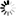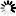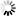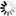
1.1/3+1/15+1/35+1/63+1/99+1/143+1/195+1/255的值是（）
    A.6/17B.6/19C.8/17D.8/19

2.有七个排成一列的数，它们的平均数是30，前三个数的平均数是28，后五个数的平均数是33。那么第三个数是（）。
    A.28B.32C.37D.39

3.1993年，一个老人：“今年我的生日已过，40多年前的今天，我还是20多岁的青年，那时我的年龄刚好等于那年年份的四个数字之和。”那么老人到2007年是多大年纪？（）
    A.75B.79C.81D.93

4.一个球从100米高处落下，每次着地后又跳回原来高度的一半再落下，当它第三次着地时，一共经过的路程为（）米。
    A.150B.200C.250D.300

5.小明家离火车站很近，他每天都可以根据车站大数的钟声起床。车站大楼的钟，每敲响一下延时3秒，间隔1秒后再敲第二下。假如从第一下钟声响起，小明就醒了，那么到小明确切判断出已是清晨6点，前后共经过了几秒钟？（）
    A.16B.18C.28D.24

参考答案解析

1.C【解析】本题可以拆项化简。如1/3=1/2(1-1/3),1/15=1/2(1/3-1/5),依此类推。

2.D【解析】28×3＋33×5－30×7＝39。

3.C【解析】1993年的40多年前应是1993－49＝1944和1993－41＝1952之间，老人那年的年龄等于当年年份四个数字之和而且是20多岁，所以应在1947至1949年之间，因为只有1947、1948、1949每个年份数字之和是20多，用年份数减四个数字之和（当年年龄）可得他的出生年份，于是1947－21＝1926，1948－22＝1926，1949－23＝1926，即他的出生年份是1926年，2007－1926＝81，即老人到2007年是81岁。

4.C【解析】本题类似于对分问题，要仔细计算，第一次下落是100，第二次下落是50米，但两次，所以也是100米。第三次是25，也是两次，所以总共为250米。

5.D【解析】从第一下钟声响起，到敲响第6下共有5个“延时”、5个“间隔”，共计（3＋1）×5＝20秒。当第6下敲响后，小明要判断是否清晨6点，他一定要等到“延时3秒”和“间隔1秒”都结束后而没有第7下敲响，才能判断出确是清晨6点。因此，答案应是：（3＋1）×6＝24（秒）。